Fuzzy system for an automatic door’s
control
In
this page you will find a fuzzy system for an automatic door’s control.
You
can play around with the applet, push “+” or “-“ to
vary the indoor expected temperature and the real temperature, press “ Pasar Persona” for you cross a person and “Pasar 5 Personas” for you cross five persons, You can see
the results using the Mandami, Product and Lucasiewicz fuzzy logics and try the
product result, also you can read a
paper describing the theory behind it.
NOTE:
You need Java Plug-in to run this applet. If it does not work, get
the latest Java Plug-in here.
It has been developed
by Joaquin Gayoso Cabada as
a final project for the course "Razonamiento
aproximado y con incertidumbre" in the Facultad
de Informática of Universidad Complutense de Madrid.
Here
is the complete paper of this project:
Fuzzy System
for Intelligent Automatic Door’s Opening Control
joaquin Gayoso Cabada, luis
garmendia salvador
gayoxo@gmail.com, lgarmend@fdi.ucm.es
Dpto. Ingeniería
Software e Inteligencia Artificial. Facultad de Informática, Universidad
Complutense de Madrid, 28040-Madrid, Spain
1.
Abstract
This paper describes an automatic door control fuzzy system based on the stream of people who walk through the door and on the difference of degrees between the indoor temperature and the outdoor temperature. The motivation of the system is to save energy by using as least as possible the door's motor and by reducing the heating waste. An implementation of the system is available in the web.
2.
Introduction
In the present world where the efficiency and the ecology
are now on top, this system tries to save on the usage of the motor by means of
an automatic control system, minimizing the impact on the environment and
reducing the energetic cost. Nowadays, when we examine usual automatic doors,
we see a manual timing system which is only controlled by the men who are
designated to set it up. In other cases, the door´s adjustment is based on the
experience of the worker who assembled the door. As a result, we may see that
automatic doors do not work properly. This common and extended used way is not
intelligent at all, because automatic doors opens too slow when there are a lot
of people walking through, or they are continuously opening and closing. There
are also situations in which the doors are closed and the air conditioner or
heating are working, while indoor and outdoor temperature is the same. As well
as open doors in midwinter when there are not too many people walking through.
Therefore, our
proposal to improve and maximize the performance of automatic doors is an
automatic fuzzy system that regulates the opening and closing based on the
following variables to set the period of time in which the door should be
keeping open.
The implementation in a Java Applet and executable java jar file is available on the web at http:/www.fdi.ucm.es/profesor/lgarmend/SC/DoorControl/
3.
Problem description
The problem is based on three variables that represent
our system: the people walking through the door, the difference of degrees
between indoor and outdoor-temperature of the building and the waiting time of
opening and closing. Normally, as we explained above, this time is adjusted by
employees without using an optimal technical method ,
so the system does not work at its fullest potential, because sometimes the
doors are very quick or too slow, and its opening and closing time is longer or
shorter than needed. It also happens the same when the indoor and outdoor-temperature
difference is too big or too small and the automatic doors are keep open or closed uselessly.
4.
Problem description with fuzzy sets
The problem description is a simplified model of the
real world door, with the following variables in the system [see Klir G. and B. Yuan, 1995; Pedrycz,
1992; Lewis, H.W. 1997].
·
Input
Variables:
o Stream of people
o
Difference
of temperature degrees
·
Output
variables:
o
Waiting
time between closing and opening.
The goal is to set a waiting time between opening and closing that minimizes the use of the motor without reducing the functionality of the door.
The following subsections describe some fuzzy sets [Zadeh, 1965] for different linguistic variables on the input and output variables.
4.1. Stream of People
The stream of people is modeled as a number of weighted people that walk through the door in a minute, it is bounded between zero and sixty. There are three linguistic variables modeled with fuzzy sets to represent the item what is represented within the figure 1. Those fuzzy sets are evaluated from a counter of people within a minute that adds one people per second when the laser of the door cuts.
The three modeled fuzzy sets to evaluate the stream of people are defined like:
§
“ Low
stream” (‘Poca’ in Spanish, in figure 1): Sigma
function with center in ten and amplitude least two.
§
“Medium stream” (‘Medio’
in Spanish): Bell function with center in fifteen and amplitude seven.
§
“High
stream” (‘Mucho’
in Spanish): Sigma function with center in thirty and amplitude least seven.
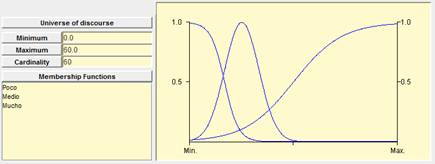
Figure 1. Fuzzy sets “low stream”, “medium stream” and “high stream” to evaluate the amount of people stream within a minute.
4.2. Difference of temperature ( in centigrade
degrees)
The
difference of temperature in centigrade degrees is a simple subtraction between
the desired indoor temperature and the real temperature out of the building.
The domain of this variable is bounded between zero and thirty. To model this
variable, it is used
four fuzzy sets because it is the most important variable, is
represented within the figure 2 and his function set are defined like:
§
“Very
low” (‘Poca’ in figure 2): Bell function with center
in zero and amplitude five.
§
“More
or less low” (‘LBaja’ in firure
2): Bell function with center in ten and amplitude five.
§
“More
or less high” (‘LAlta’ in figure 2): Bell function
with center in fifteen and amplitude five.
§
“High”
(‘Mucho’ in figure 2): Sigma function with center in twelve and amplitude
three.
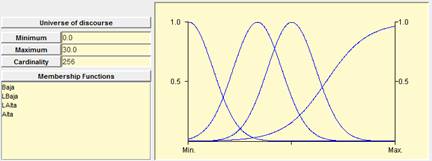
Figure 2. Fuzzy sets “very low”, “More or less low”, “more or less high”, and “high” to evaluate the difference of temperature in centigrade degrees.
4.3. Open waiting time between closing and opening the door
The waiting time between closing and opening of the door is designed to model a subjective vision of the waiting time concept in seconds. It can be readjust by experts based on air cooling and warming on temperature differences.
We use five fuzzy sets represented within figure 3 to model this variable:
§
“Very
low” (‘Bajo’ in Spanish): Bell function with center
in zero and amplitude one.
§
“Low”
(‘Leve’ in Spanish): Bell function with center in two
and amplitude one.
§
“Medium”
(‘Medio’ in Spanish): Bell function with center in
four and amplitude one.
§
“Some” (‘Moderado’ in Spanish): Sigma function with center in six
and amplitude two.
§
“High”
(‘Alto’ in Spanish): Isosceles function with center in thirty and amplitude
thirty.
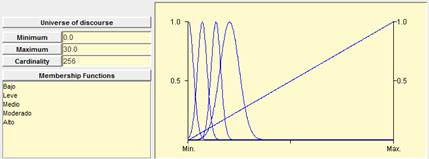
Figure 3. Fuzzy sets “Very Low”, “Low”, “Medium”, “Some”, “High” for the waiting time ins seconds.
5.
Fuzzy Rules for door’s control
Once we have modeled the fuzzy sets, we define rules that represent the desired functionality to learn how many seconds to maintain open the door from the people stream and the difference of temperature. Twelve rules are represents in an adjacency table (figure 4), where DifTemp= Difference of temperature, Personas= Stream of People, (X, Y) = Waiting Time Door.
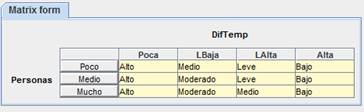
Figure 4. FuzzyRules of the system.
For example, the rule described in (first row, first
column) is the fuzzy rule: IF ‘the
people stream is Low’ AND ‘the difference of temperature is Very Low’ THEN ‘the
opening time is high”
6.
Results of applying our control to a
door
We apply our control to a door and we realize that the
door can save so much energy if the difference of temperature is too high and
modeled if the difference is middle based on the stream of people.
The AND operator in the premise is tested for
different continuous t-norms [B. Schweizer and A.Sklar, 1960]. We only test
continuous t-norms because we want a ‘soft’ behavior, in the sense that if the
difference of temperature is increased a little bit, the door´s open wait must
be decreased just a little bit, so we do approximate reasoning. After testing
the AND operator with several t-norms we find that the minimum t-norm ignores
one of the two input variables loosing then some king of information. The
Lucasiewicz t-norm gives a too low premise evaluation when both variables are
not close to one, so it is chosen an `in between’ product t-norm, which also provides a softer
behavior and its bound results represent
better the problem.
The chosen implication operator is Mandami´s operator
[Mandami, 1977].
With the chosen operators, a summary of the fuzzy
inference results are shown in figure 5.
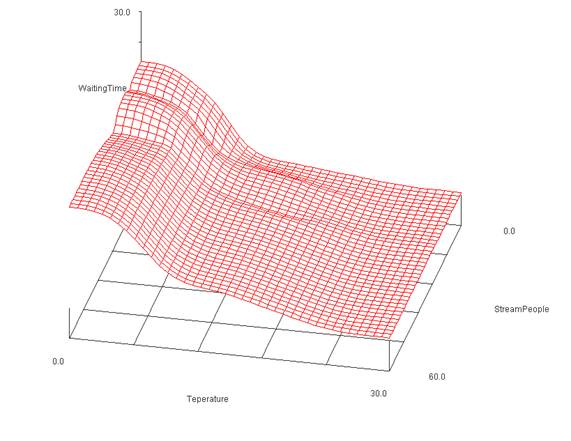
Figure 5. Waiting time learned from people stream and temperature difference using the product t-norm in the premise conjunction and the Mandami´s implication operator.
7.
Fuzzy System VS Singleton System
We implement a classical rule inference system to
compare the difference between the fuzzy approach and the classical rule system
approach. The crisp sets are defined with the same names that in the fuzzy
case, but they only have nitide values 0 or 1. The crisp sets are used in the
classical rule systems are shown in figures
6, 7, 8.
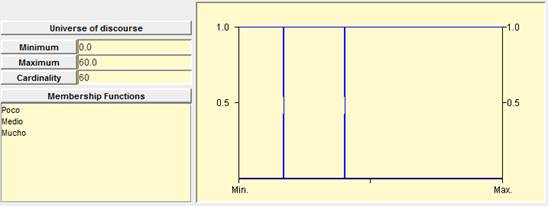
Figure 6. Three stream of people classical sets for “low stream”, “medium stream” and “high stream”.
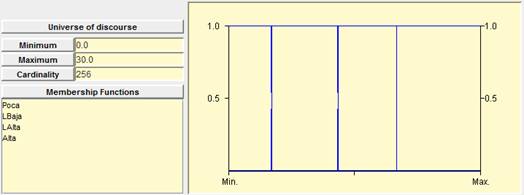
Figure 7. Four Difference of temperature classical sets for “very low”, “More or less low”, “more or less high”, and “high”.
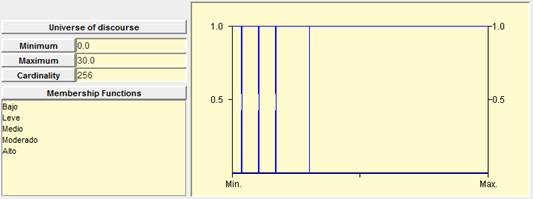
Figure 8. Five waiting time classical sets for “Very Low”, “Low”, “Medium”, “Some”, “High” for the waiting time ins seconds.
Then we apply the same rules described in figure 4,
now considered nitide rules and we reach the following learned waiting time
described in figure 9.
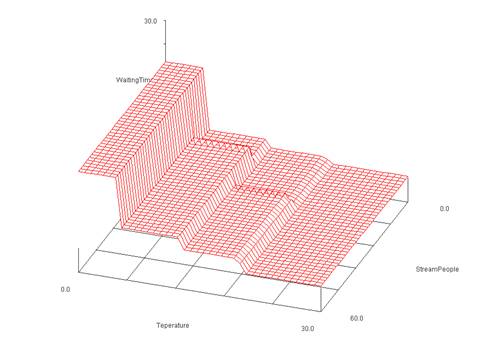
Figure 9. Opening waiting time learned from classical rules of inference.
8.
Conclusions
The given intelligent
system to learn how long a door
must be open can save a lot of energy
used by the motor of the door and preserving indoor temperature if the door is
implanted in cities with a medium fluctuating temperature and different streams
of persons along the time that the building is opened.
A fuzzy and a classical rule of inference systems have
been compared. Examining the figures 5 and 9 we find that in extreme conditions
(nitide values) both systems behave in a similar way, but when somehow
uncertainty appears, the fuzzy system
reaches a big improvement , and have a much ‘softer’ behavior than the
classical modus ponens inference system, that produces some ‘jumps’ in the
inference results. When the premise conjunction is implemented with the product
t-norm operator, softness of the system is increased when it is compared with
other continuous conjunction operators.
The implementation in Java of the fuzzy inference engine can be tested at http://www.fdi.ucm.es/profesor/lgarmend/SC/DoorControl/
9.
References
1. IMSE
Centro Nacional de Microelectrónica. Herramientas de CAD para Lógica Difusa. Xfuzzy 3.0. http://www.imse.cnm.es,
2003.
2. Klir G. and Yuan, B. “Fuzzy Sets and Fuzzy Logic Theory
and its Applications” Prentice Hall. 1995.
3. Pedrycz, W.: Modelling with fuzzy
sets in fuzzy control. Fuzzy Days, 3-34, 1992.
4. Lewis, H.W. “The Foundations of Fuzzy Control”,
Springer. 1997.
5. E. H. Mamdani,
"Applications of Fuzzy Set Theory to Control Systems: A Survey," in
Fuzzy Automata and Decision Processes, M. M. Gupta, G. N. Saridis
and B. R. Gaines, eds., North-Holland, New York, pp. 1-13, 1977.
6. B. Schweizer and A.Sklar, Probabilistic Metric Spaces.
North-Holland, 1960.
5. E. Trillas and L. Valverde,
Approximate reasoning in expert systems, North-Holland, 157-166, 1985.
7. L.A. Zadeh, Information and Control, 8, 338-353, 1965.