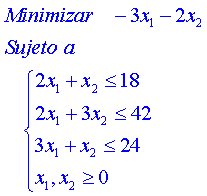
Capítulo 3 - Bases matemáticas y computacionales
Como vimos en la introducción y en los objetivos de nuestro trabajo, hemos planteado el modelo matemático de la red de gasoductos como un problema de optimización con restricciones, es decir, constituido por una serie de variables de decisión, una función objetivo, y un conjunto de restricciones sobre las variables. En concreto hemos utilizado la programación lineal entera-mixta (MILP) sobre un resolutor comercial (CPLEX) con la ayuda de un lenguaje algebraico de modelado (OPL). Los resolutores MILP comerciales en general, y CPLEX en particular, han conseguido un elevado grado de eficiencia. Revisaremos en este capítulo el funcionamiento interno de la resolución de problemas MILP.
Los problemas MILP se resuelven utilizando métodos de bifurcación y acotación (Branch&Bound), es decir, resolviendo en cada nodo del árbol de búsqueda los sub-problemas de programación lineal (LP) que se generan al relajar alguna de las restricciones enteras. La relajación permite obtener límites (cotas) a los valores de la función objetivo. La eficiencia en la resolución de estos problemas dependerá, pues, en primer lugar de la eficiencia en la resolución de los problemas lineales (simplex), y en segundo lugar de la eficiencia al recorrer el árbol de búsqueda (bifurcación y acotación)
Revisaremos, pues, las bases de estos dos algoritmos así como la expresión MILP de algunas restricciones no lineales que aparecen en el modelo matemático de la red de gasoductos. También revisaremos el lenguaje de modelado y el resolutor utilizados para expresar y resolver el problema MILP.
Los dos algoritmos básicos que forman parte del resolutor de CPLEX son el Simplex y el branch&bound. En efecto, nuestro modelo cuenta con parte entera y parte real: para resolver problemas de programación lineal continua se utiliza principalmente el algoritmo del Simplex; y para la parte de programación lineal entera, se opera mediante métodos de bifurcación y acotación (branch&bound). Estos métodos se potencian además con la introducción de planos de corte, dando lugar a los métodos de bifurcación y corte (branch&cut).
Así, el algoritmo de branch&bound realizará relajaciones lineales de las restricciones enteras, dejando de imponer el carácter entero de las variables que lo sean; y estos subproblemas se resolverán mediante el algoritmo del Simplex.
3.1.1 Programación lineal: método del Simplex
El teorema fundamental de la programación lineal asegura que, si un problema tiene solución óptima finita, entonces existe por lo menos un punto extremo de la región factible en el cual se alcanza dicha solución óptima. Así, siempre se podrá resolver un problema de este tipo evaluando la función objetivo en un número finito de puntos. El problema reside en que dicho número puede ser muy elevado, por lo que se hace necesaria una estrategia que recorra estos puntos de manera eficiente, y que disponga de un criterio que determine si se ha alcanzado la solución óptima, sin necesidad de recorrer todo el espacio de búsqueda.
Vamos a introducir el método
del Simplex de una manera intuitiva utilizando el siguiente ejemplo:
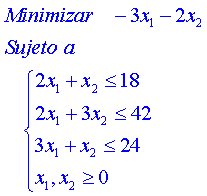
En primer lugar, se introduce
la variable z a minimizar, y las variables de acoplo a, b y
c, para escribir las inigualdades como igualdades. Reescribimos entonces el
problema y comienza la resolución, que parte de una base inicial, y va pasando,
en sucesivas iteraciones, por bases de mejor coste hasta alcanzar el óptimo.
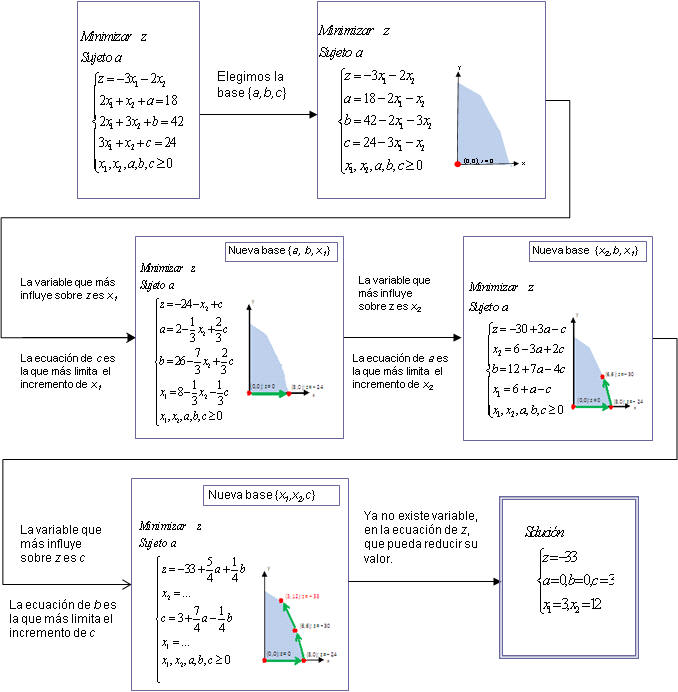
3.1.2 Programación lineal entera-mixta: método de Branch&bound
Un problema de programación
lineal entera mixta (MILP) tiene la siguiente estructura:
Este método realiza una búsqueda de la solución en una secuencia de procesos en los que se intercalan dos fases: la bifurcación sobre los valores de una variable de decisión entera, y la acotación del espacio de búsqueda. Para ello realizan relajaciones lineales del problema, lo cual permite ir descomponiendo el problema en sub-problemas de menor tamaño, descartando paulatinamente aquellos cuya función de coste exceda el valor de la mejor solución entera encontrada hasta ese momento. La relajación lineal y la búsqueda son, en efecto, los dos procesos fundamentales de los métodos de branch&bound y los determinantes de la eficiencia de su ejecución.
A lo
largo de la resolución se recorre así un árbol de búsqueda, que se va generando
al relajar las restricciones enteras y resolver en cada nodo sub-problemas de
programación lineal (LP), como se muestra en el ejemplo siguiente, en el cual,
en cada nodo, se aplicaría el método del Simplex a los sub-problemas del
original. A continuación se ilustra este método para un MILP sencillo.
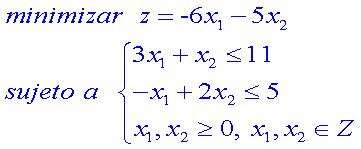
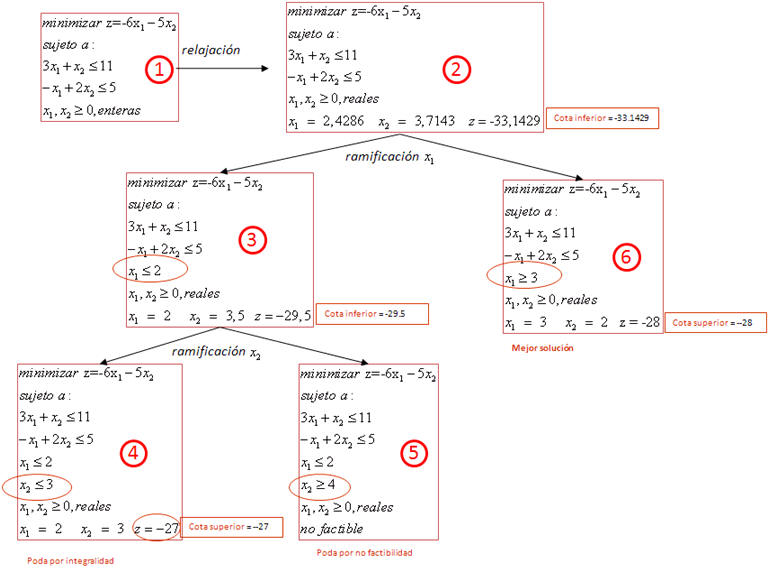
La relajación lineal permite así ir obteniendo límites para los valores de la función objetivo. El árbol se construye y se recorre con los siguientes criterios:
Existen procedimientos para mejorar la eficiencia de esta búsqueda, como es la introducción de planos de corte en el método de branch&cut, lo cual reduce el árbol de búsqueda, y acelera por tanto la resolución. CPLEX integra estos y más algoritmos de optimización.
Además, con los ordenadores actuales, cuyos procesadores pueden constar de más de un núcleo, se podrán aprovechar las características de este algoritmo, haciendo que cada uno de los núcleos recorra una rama diferente del árbol, reduciéndose de manera notable el tiempo de cómputo.
3.2 Linealización de restricciones
Entre las restricciones que
necesitamos para modelar el sistema, tendremos algunas no lineales, como resulta
ser, por ejemplo, la relación entre el flujo dentro de un gasoducto y las
presiones. Para integrar estos comportamientos no lineales en el modelo,
deberemos aproximar dichas relaciones, describiéndolas mediante restricciones
lineales. A continuación se describe la estrategia escogida para aproximar
funciones de dos variables de tipo z = f(x, y): se definirá
una malla de valores (x, y), para los cuales conocemos el valor de la
variable z. El sistema deberá entonces asociar pesos a cada punto de la
malla, para determinar una terna de valores consecuente con los valores
conocidos, considerando que la relación entre las tres variables es lineal entre
dos puntos consecutivos de la misma. Esto se consigue definiendo en primer lugar
las variables como sigue:
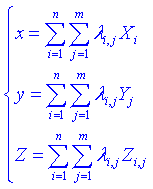
(3.1)
siendo n y m la longitud de los vectores {Xi, Yj} respectivamente, que son los valores de (x, y) en cada punto de la malla; y Zi,j el valor de la función f(x, y) correspondiente a dichos puntos.
λi,j denotan
los pesos que el sistema debe adjudicar para realizar la aproximación. Estos
pesos deben entonces ser positivos y sumar 1, además de cumplir una
restricción de tipo SOS2 por filas, columnas y diagonales. Esta restricción
impone que a lo sumo dos de los pesos son distintos de cero, y, en caso de ser
efectivamente dos, éstos han de ser consecutivos. Así, el valor de cada variable
se estará escogiendo mediante una interpolación lineal entre los dos valores
conocidos más cercanos. Como hemos visto, en el lenguaje de programación
utilizado no contamos con la restricción SOS2, de modo que la modelaremos como
sigue, mediante las variables auxiliares Γ
y
γ, esta última binaria, para las filas, y, de forma análoga, variables de
este tipo para la columnas y las diagonales. A continuación se muestra la
implementación para las filas, la de las columnas y diagonales será análoga.
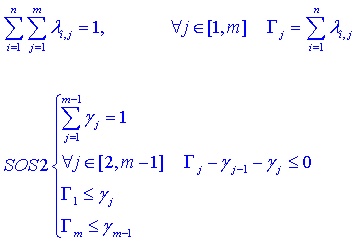
(3.2)
3.3 Resolutor y lenguaje de modelado utilizados
A la hora de implementar el modelo, hemos escogido el lenguaje algebraico de modelado OPL (Optimization Programming Language), diseñado para facilitar la expresión de problemas de programación matemática continua y entera (MP). Este tipo de lenguaje permite expresar el modelo con una sintaxis próxima a la propia especificación matemática, y las modificaciones y ampliaciones del modelo resultan relativamente sencillas de realizar, permitiendo una estrategia incremental de desarrollo del modelo.
Se ha utilizado así un resolutor comercial, ILOG CPLEX para implementar el modelo. CPLEX dispone en efecto de un motor de resolución que está reconocido por la comunidad de investigación operativa y usuarios de grandes compañía,s como el motor de optimización más eficiente de programación lineal, tanto por la velocidad de ejecución como por el tamaño de los problemas que resuelve. La eficiencia de CPLEX es en efecto debida a la especialización de los algoritmos y pre-resolutores que utiliza, así como a la adaptación de dichos algoritmos a las nuevas arquitecturas de los procesadores, que explotan cada vez más el paralelismo: con los ordenadores actuales, cuyos procesadores pueden constar de más de un núcleo, se podrán aprovechar por ejemplo las características del Branch&bound, haciendo que cada uno de los núcleos recorra una rama diferente del árbol, reduciéndose de manera notable el tiempo de cómputo.
Capítulo 2: Bases físicas de la red básica de gasoductos
Capítulo 3: Bases matemáticas y computacionales
Capítulo 6: Conclusiones y trabajos futuros