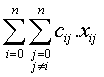
En nuestro caso vamos a optimizar, inicialmente, la distancia recorrida por los vehículos de recogida de residuos urbanos, abordándolo desde el punto de vista de la programación lineal entera-mixta (MILP).
Tenemos diferentes Municipios de la provincia de Huelva y varias Estaciones de transferencias, de manera que cada municipio tiene asignado una de ellas. Los vehículos de recogida se agrupan en Bases en las que existen un número determinado de vehículos de igual o diferentes características que tienen asignado la labor de la recogida de los residuos sólidos con una zona de actuación (municipios) previamente determinada.
Dadas las características del servicio no se consideran ventanas de tiempo.
De esta manera nuestro problema se subdivide en diferentes problemas similares en los que tene-mos un grupo de municipios asociados, inicialmente a una única Base de Vehículos y esta con un grupo determinado de vehículos llevarían los residuos recogidos a una o varias Estaciones de Trans-ferencia.
Vamos a partir del algoritmo más sencillo posible basado en el que resuelve el problema del viajante y lo iremos adaptando poco a poco a las especificaciones del problema completo. El problema del viajante consiste en lo siguiente: un viajante tiene que visitar un número determinado de ciudades de manera que visite todas pasando por cada una de ellas una vez y regresando al punto de partida al terminar.
Sea cij el coste de ir del punto i al j. xij es una variable binaria que tiene el valor 1 si después de visi-tar el punto i visita el j y 0 en el resto de los casos.
El objeto de nuestro modelo es por tanto minimizar el coste (p.e. distancia) total al recorrer todos los puntos. Es decir minimizar:
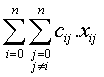
Siendo el punto 0 el de partida y de término y 1..n los n puntos (poblaciones) a visitar.
Las primeras condiciones que debe cumplir el modelo es que desde un punto i cualquiera solo se vaya a uno y solo uno j:
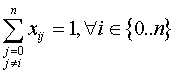
Y que a un punto cualquiera j solo se pueda llegar desde uno y solo uno i:
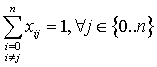
En este punto nos surge el primer problema: se podrían dar varios circuitos independientes, por ejemplo si tenemos que recorrer siete puntos (del 1 al 7) partiendo del punto 0, se podría dar el recorrido 0 → 2, 2 → 0, 5 → 3, 3 → 5, que no es lo que queremos. Para evitar esto añadimos una tercera condición:
![]()
Siendo ui y uj variables auxiliares enteras.
Ya tendríamos el modelo que resuelve el problema del viajante. Saldría del punto 0 y recorrería los n puntos formando un ciclo. Con este sencillo planteamiento ya nos puede dar una idea de la com-plejidad computacional que esconde su resolución. Este modelo tiene las siguientes variables: n.(n+1) variables xij y n variables ui. Y las siguientes restricciones: (n+1) de la primera, (n+1) de la segunda y n.(n-1) de la tercera. Para hacernos una idea, si tenemos 70 poblaciones y una única estación de transferencia estamos hablando de 5.040 variables y 4.972 restricciones.
En nuestro caso habría que añadir algunas variantes que nos implica otras restricciones. Empece-mos por el número de vehículos. Antes era una sola persona o vehículo quien recorría todos los puntos, pues bien, en nuestro caso es un grupo de vehículos los que se reparten la ruta. Así pues, añadimos esta variante. Ahora tendríamos tantas rutas como vehículos. Estamos en un problema de VRP (Vehicle Route Problem)
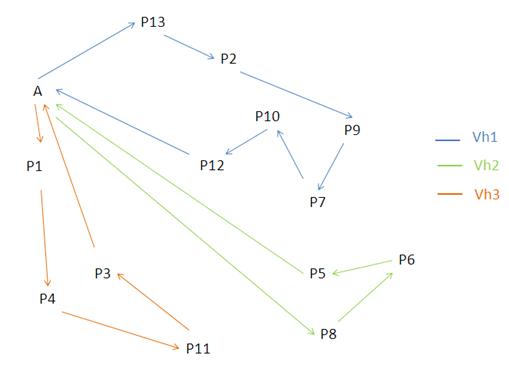
Figura 3.1: Esquema VRP para tres vehículos
Vemos en la figura 3.1 un caso para tres vehículos. Para la formulación introducimos otro subíndice: el vehículo. Ahora la función a minimizar quedaría así:
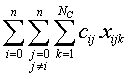
Siendo k el nuevo subíndice y NC el número de vehículos.
Si mantenemos las dos primeras restricciones como están para cada vehículo, estaríamos obligando a que todos los vehículos recorrieran todas las poblaciones, recogieran o no basura en cada una de ellas, situación que estaría en contra de nuestro objetivo de optimización. La obligatoriedad de re-correr todos los puntos la corregimos cambiando el signo “=” de las dos primeras restricciones por el “≤”, de manera que también admitamos el 0, es decir, que no tenga que existir un trayecto i, j para un vehículo determinado.
En este punto, el modelo podría no hacer ningún recorrido, ya que solo le estamos pidiendo que mi-nimice el coste, y ahora lo cumpliría si no sale ningún vehículo.
Introducimos la condición impuesta por la demanda: la basura generada por los municipios hay que recogerla en su totalidad.
Para esto tenemos que introducir nuevas variables, en este caso asociadas a cada población. Y ade-más un nuevo parámetro: la demanda, es decir, la basura generada por cada municipio.
Sea yjk la variable (real o entera) que nos indica la cantidad de basura que el vehículo k recoge del municipio j. RMj sería la cantidad de basura generada por el municipio j.
La cuarta restricción que habríamos que añadir sería la obligatoriedad de recoger toda la basura:
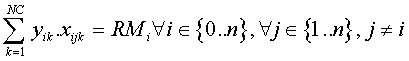
Que no es lineal y que lógicamente habría que linealizar al implementar el modelo.
En este momento se recoge toda la basura y los vehículos van (x) donde recogen (y). El problema que nos surge ahora es que al suavizar las dos primeras restricciones ya no estamos obligando a realizar el recorrido completo, por ejemplo, los siguientes recorridos son válidos:
0 → 5, 5 → 2, 1 → 4 con el vehículo 1 y 0 → 3, 2 → 1 con el vehículo 2 y la basura la recogen: el vehículo 1: municipios 2, 4 y 5; vehículo 2: 1 y 3. Esto cumple con las condiciones impuestas actual-mente pero observamos que:
1. los tramos no son consecutivos,
2. estamos en municipios dónde no recogemos basura y
3. no terminamos en el punto inicial.
Luego las condiciones impuestas no son suficientes. Podríamos imponer la siguiente restricción para que los tramos sean consecutivos y así resolvamos el primer inconveniente:
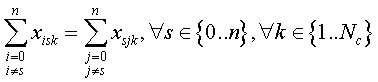
Con esta restricción hemos corregido el punto 1. Dejamos pendiente, de momento, los puntos 2 y 3.
Al no tener la capacidad de los vehículos limitada, podríamos hacer todo el recorrido con un solo vehículo. Introduzcamos ahora la limitación de la capacidad de los vehículos haciendo que la suma de las cantidades recogidas por los vehículos no supere su capacidad máxima:
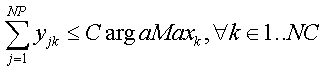
siendo CargaMaxk la carga máxima que tiene permitida el vehículo k
El problema que nos encontramos ahora es que la suma de las capacidades máximas de los vehícu-los no tiene por qué ser igual o superior a la demanda y, por tanto, estaremos obligados a aumentar el tamaño de la flota o, lo que es más operativo, hacer varios viajes con cada vehículo hasta satisfacer la demanda.
Establezcamos ahora una cota en el número máximo de viajes por vehículo: NV, e introduzcamos un nuevo subíndice: v, el número de viaje de cada vehículo. La función a minimizar nos quedaría ahora de la siguiente manera:
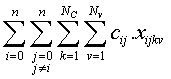
Las dos primeras restricciones nos quedaría de la siguiente manera:
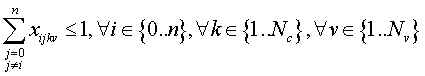
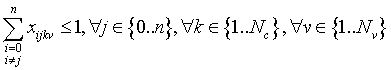
La tercera restricción quedaría así:
![]()
La cuarta restricción todavía sin linealizar quedaría así:
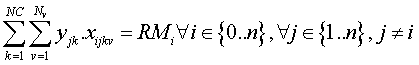
Los vehículos no pueden trabajar todo el tiempo que deseemos, sino que hay que restringir su uso. El límite puede ser debido a diferentes causas:
- Si el vehículo es conducido por un único conductor podemos establecer cómo límite de uso diario las horas máximas diarias que el convenio permite
- Si el vehículo es de contratación externa, estableceremos el límite de la contratación
- Si se establecen turnos de conductores podríamos establecer el máximo en 24 horas.
Pero lo cierto es que no hay una regla para todos los vehículos, por lo que cada vehículo tendrá un límite superior particular. El tiempo se emplea fundamentalmente en el recorrido, no obstante tenemos que tener en cuenta otros componentes, como el tiempo de recogida del contenedor o el de vaciado del vehículo.
Si disponemos de los tracks actuales podemos determinar los parámetros necesarios, como por ejemplo la velocidad media entre poblaciones o el tiempo medio de recogida de un contenedor. El tiempo de vaciado del camión lo establecemos como la diferencia entre el momento en el que el vehículo cargado entra en la estación y el momento en el que sale vacío para realizar un nuevo viaje.
La restricción debida al tiempo de recorrido sería:
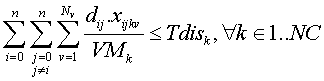
Siendo VMk la velocidad media en carretera de cada vehículo, Tdisk el tiempo de disponibilidad de cada vehículo, añadiéndole los tiempos transcurridos en el interior de cada población, de recogida de contenedores y de vaciado.
Seguimos sin corregir los problemas 2 y 3 anteriores. Empecemos por el 3: para que los vehículos vuelvan a la estación de transferencia que es de donde salieron, imponemos la siguiente restricción:
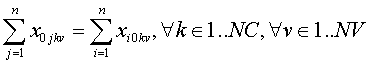
El primer miembro representa la salida y el segundo la llegada. Si el primer miembro vale 1 (el ve-hículo en ese viaje salió) el segundo miembro también valdrá 1 (el vehículo en ese viaje, regresa).
Solo nos queda corregir el punto 2, es decir, el vehículo va a un Municipio si es para recoger basura:
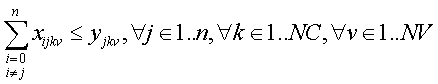
El modelo así definido podríamos considerarlo completo.
Otra consideración es fijar el criterio a optimizar. Hemos supuesto inicialmente la distancia reco-rrida por ser el valor que posiblemente más influya en el coste. Si queremos minimizar el coste deberíamos introducir en el modelo otras consideraciones. La distancia recorrida sería fácil pasarla a coste introduciendo el parámetro de consumo medio o mejor el coste por kilómetro que ya incluye los mantenimientos y reposiciones de piezas de uso.
Existirían otros costes no relacionados con el uso del vehículo como por ejemplo su disponibilidad, que por el hecho de estar preparado el vehículo en el garaje con su conductor tiene un coste. En este coste podemos considerar el salario del conductor, la amortización del vehículo, impuestos y seguro. Al considerar estos costes el modelo debería preferir maximizar el número de viajes de un vehículo que aumentar el número de vehículos.
Vamos a trabajar con un parámetro que llamaremos factor de compresión que engloba varios con-ceptos. Lo vamos a definir como el volumen (m3) que alcanza el contenido de un contenedor dentro del camión una vez prensado. Intervienen varias variables:
- el volumen del contenedor,
- la capacidad de prensado del sistema de recogida del vehículo y
- lo lleno o vacío que esté el contenedor en el momento de su recogida.
Este último aspecto depende fuertemente de la estacionalidad ya que en verano y en invierno pue-den existir el mismo número de contenedores pero su llenado es claramente diferente, especial-mente en las zonas costeras. Este parámetro lo vamos a trabajar desde la hoja de cálculo auxiliar de donde CPLEX lee únicamente el número de contenedores que un vehículo en particular puede re-coger, dejando la tarea de la conversión de la capacidad del vehículo al número de contenedores, a través del factor de compresión, a esta hoja. Para cada sistema de recogida y para estación lo cal-cularemos de forma empírica aprovechando las estadísticas actuales.
Para el planteamiento de la estacionalidad vamos a suponer que el número de contenedores es el mismo y que solo cambian dos valores:
· Existencia o no de vehículos de refuerzo en época estival
· Factor de compresión (menor en época estival)
Capítulo 2: Especificación del problema
Capítulo 3: Modelo MILP básico