Capítulo 4. Refinado del modelo básico

La metodología que vamos a utilizar será implementar de forma sucesiva modelos cada vez más ajustados a las características del problema. Iremos describiendo, en cada modelo, las caracterís-ticas que lo definen.

En el primer y segundo modelo definimos una única Base y Estación de Transferencia. En el primero la hacemos coincidir, despreciando el desplazamiento entre ambas, haciendo que los recorridos empiecen y terminen en la Estación de Transferencia. En el segundo modelo, sin embargo, ya los vehículos parten de la base, donde también terminan su jornada aunque descarguen siempre en las Estaciones de Transferencia. El tercer modelo usa una única Base de vehículos pero con dos Estacio-nes de Transferencia. En este modelo estableceremos dos variantes, una primera en el que no for-zamos el uso de ambas Estaciones y una segunda en que si lo hacemos. El cuarto modelo, el más completo del estudio, se plantea con una única base de vehículos y con un número variable de Estaciones de Transferencia. Con este cuarto modelo se podrían abordar todos los casos.

Primer MODELO

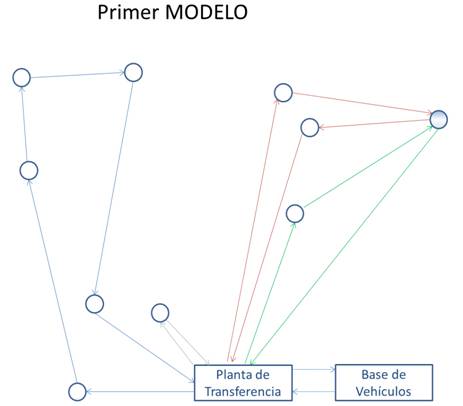
Figura 4.1: Esquema Primer Modelo

Consideraciones particulares del modelo:

En este primer modelo, que mostramos en la figura 4.1, introducimos las siguientes consideraciones particulares:

- la función objetivo será principalmente la distancia recorrida por los vehículos de recogida (modificada, como ya veremos)

- considerando que los vehículos parten y terminan en las Estaciones de transferencia o Bases de vehículos, ya que estas, supuestamente, coincidirían. El supuesto obliga a que los vehícu-los vayan y vuelvan de las Estaciones de Transferencia, reduciendo el tiempo disponible en el empleado en recorrer este tramo. La distancia y el tiempo empleado entre la Estación de Transferencia y la Base de Vehículos se desprecia.

- No se considera la distancia recorrida ni el tiempo dentro de las poblaciones

A este supuesto podríamos aproximar las siguientes Bases que trabajan con una Estación de Trans-ferencia exclusivamente:

BASE	ESTACIÓN DE TRANSFERENCIA
Aracena	Linares de la Sierra
Condado	Villarrasa
Cuenca Minera	El Campillo
Isla Cristina	La Redondela

Tabla 4.1: Bases de vehículos asociadas al Primer Modelo

En estos casos todos los vehículos y contenedores son del mismo tipo: de carga trasera.

No se tendrá en cuenta otros criterios de coste.

Los índices indican los municipios desde el 1 al NP, siendo NP el número de municipios a considerar en el caso. El subíndice 0 se reserva a la estación de transferencia, de donde salen los vehículos y donde vuelven para su vaciado y, si acaso, vuelta a salir con el vehículo vacío.

Cuando el índice vaya de 1 a número de poblaciones hablaremos de poblaciones o municipios y cuando el índice vaya de cero al número de poblaciones hablaremos de puntos (que incluiría la esta-ción de transferencia y los municipios).

Usaremos los subíndices i y j para las poblaciones y estación de transferencia, k para los vehículos y v para los viajes.

El número de vehículos no se optimiza sino que entra al modelo como parámetro.

PARÁMETROS

NP	int	Número de poblaciones o municipios
NC	int	Número de vehículos asociados a la Estación de Transferen-cia
NV	int	Número máximo de viajes por vehículo
*d_ij*	float	Distancia entre el el punto i al j. Tanto i como j van desde 0 a NP. En kilómetros
TR	float	Tiempo (en horas) que se tarda en recoger un contenedor
*RM_i*	int	Cantidad de basura generada en la población i. En número de contenedores. i entre 1 y NP.
U	int	Cota superior de RM(i)
*CargaMax_k*	int	Carga máxima de cada vehículo en número de contenedores; k entre 1 y NV
*TJor_k*	int	Tiempo (horas) máximo de disponibilidad de cada vehículo
*VM_k*	float	Velocidad media de cada vehículo en carretera
*T_Vaciado*	float	Tiempo que tardamos en dejar el camión listo para la si-guiente recogida
*PesoNumViajes*	Int	Valor utilizado con la variable n_viaj en la función objetivo
*PesoNumVisitas*	int	Valor utilizado con la suma de las variables n_vis_j en la fun-ción objetivo

VARIABLES DE DECISIÓN

*x_ijkv*	bin	Si es 1, el vehículo recorre el tramo del punto i al j, entrando en ambos lugares que, si son municipios, es para recoger basura. Tanto i como j varían entre 0 y NP.
*y_jkv*	Int	Cantidad de basura (número de contenedores) que el vehículo k en el viaje v recoge del municipio j; j varía entre 1 y NP
*u_j*	Int	Variable auxiliar que utilizamos para evitar subitinerarios desco-nectados
*z_ijkv*	int	Variable auxiliar que utilizamos para linealizar una restricción; i varía entre 0 y NP, j entre 1 y NP

VARIABLES AUXILIARES

Estas variables las utilizamos para recoger datos que nos indican el funcionamiento del servicio y que normalmente las volcamos en la hoja de cálculo auxiliar.

*t_rec_kv*	float	Tiempo empleado, exclusivamente en el recorrido, por cada ve-hículo k en cada viaje v:
*t_con_kv*	float	Tiempo empleado por cada vehículo (k) en recoger todos los contenedores durante un viaje (v):
*t_vac_k*	float	Tiempo que emplea cada vehículo en estar disponible:
*t_veh_k*	float	Tiempo total empleado por cada vehículo:
*c_veh_kv*	int	Basura (número de contenedores) recogida por un vehículo (k) en cada viaje (v):
*d_veh_kv*	float	Distancia recorrida (en kms) por el vehículo k en cada viaje v:
*d_Recorrida*	float	Distancia recorrida por todos los vehículos:

*y_TV_ik*	int	Cantidad recogida en cada municipio por población y vehículo. Almacenamos el número de contenedores que recogemos por cada camión y en cada municipio:
*n_viaj*	int	Número total de viajes. Es el número total de viajes realizados por todos los vehículos:
*n_vis_j*	Int	Número de visitas a la población. El número de veces que una población es visitada por camiones para que le recogen toda o parte de la basura:

FUNCIÓN OBJETIVO

Minimizar la distancia recorrida por todos los vehículos en todos los viajes que realicen para recoger los residuos influenciada con el número de vehículos y de viajes. Es decir, tenemos que minimizar la siguiente función de coste:

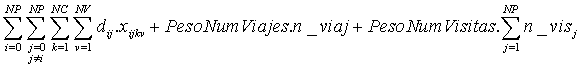
Para poder monitorizar algunos valores vamos a descomponer la función:

Minimizar d_Recorrida, siendo esta:

RESTRICCIONES

RESTRICCIÓN 01: Solo una rama de salida

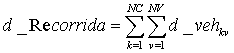
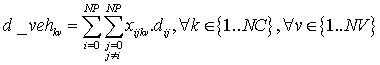
Desde cualquier punto solo podremos ir a otro, con un determinado vehículo y viaje:

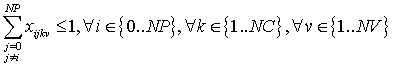
RESTRICCIÓN 02: Solo una rama de llegada

A cualquier punto solo podemos llegar desde uno, con un determinado vehículo y viaje:

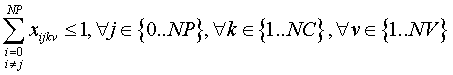
RESTRICCIÓN 03: Recorridos inconexos

Para evitar recorridos inconexos como 3 → 7, 7 → 3 y 0 → 4, 4 → 8, 8 → 9, 9 → 0. Lo que evitamos con esta restricción es que si un tramo i-j se recorre no se pueda hacer el inverso: j-i. Hemos excep-tuado el índice 0 ya que si admitimos ir desde la estación de transferencia a un municipio y volver:

RESTRICCIÓN 04: Gestión de la demanda

Se ha de recoger toda la basura generada en cada municipio. La suma de los productos de y_jkv (can-tidad de basura que el vehículo k en su viaje v recoge del municipio j) por x_ijkv (que nos indica que el vehículo k en su viaje v llega al municipio j procedente del punto i) para todos los vehículos y duran-te todos los viajes sebe ser igual a la demanda del municipio j. Es necesario multiplicar los valores de y por x para que esta variable no trabaje de forma independiente de x. Si no lo hiciéramos así, estaríamos contabilizando basura recogida de los municipios sin haber pasado por ellos:

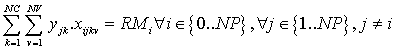
El problema que nos encontramos es que el producto de dos variables (una entera y la otra bi-naria) ya no nos permite plantear un sistema de ecuaciones lineales. Podemos cambiar esta restricción por las siguientes cuatro restricciones lineales, utilizando una variable auxiliar z:

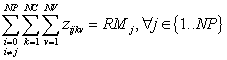
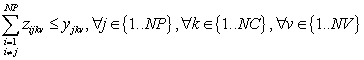
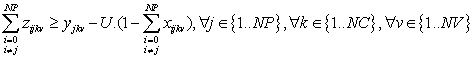
RESTRICCIÓN 04-B: Gestión de la demanda. No la utilizo (LINEAL)

En vez de la restricción anterior, esta opción es más sencilla:

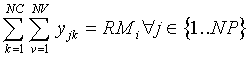
Y para evitar que x valga continuamente 0 a pesar de valer y > 0:

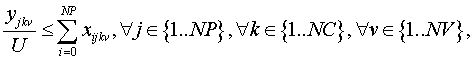
Siendo U una cota superior de RM

RESTRICCIÓN 05: No ir sin recoger

Para evitar recorrer lugares donde no se recoge basura, es decir para evitar situaciones como : (no recojo basura a pesar de haber llegado):

RESTRICCIÓN 06: Ramas muertas

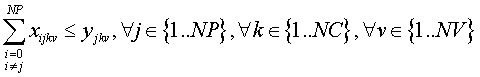
Para evitar tramos de recorridos que no sean consecutivos, es decir llegar a un municipio determi-nado y luego no salir de él. Impondríamos la siguiente restricción:

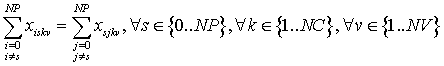
Que viene a indicar que para un vehículo y viaje determinado, salgo del municipio s si y solo si llego a él.

RESTRICCIÓN 07: Capacidad de los vehículos

Introduzcamos ahora la limitación de la capacidad de los vehículos haciendo que la suma de las cantidades recogidas por los vehículos no supere su capacidad máxima:

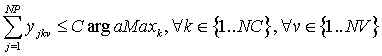
En cada viaje de cada vehículo, todas las cantidades de basura recogidas en los diferentes munici-pios no pueden superar la capacidad máxima del vehículo. Esta restricción la vamos a descomponer para poder dejar registro de las cantidades recogidas:

RESTRICCIÓN 08: Tiempos

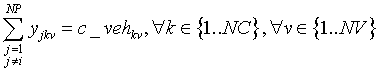
El tiempo que emplea cada vehículo no puede superar su tiempo de disponibilidad, que si va asociado a un conductor específico, este tiempo coincidiría con la jornada de trabajo. El tiempo lo emplea en:

i. Recorrer desde la estación de transferencia al primer municipio, recorrer los municipios donde recoge basura, regresar a la estación. (t_rec):

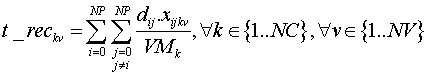
ii. Recoger los contenedores (t_con):

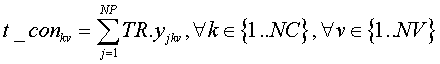
iii. Preparación de camión para su uso en el siguiente viaje (vaciar la basura, fundamentalmente) (t_vac):

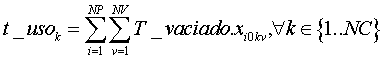
La restricción sería:

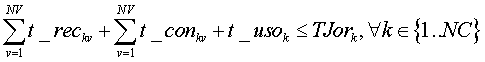
RESTRICCIÓN 09: Vuelta a la estación

Para que los vehículos vuelvan a la estación de transferencia que es de donde salieron, imponemos la siguiente restricción:

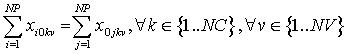
El primer miembro representa la salida y el segundo la llegada. Si el primer miembro vale 1 (el vehí-culo en ese viaje salió) el segundo miembro también valdrá 1 (el vehículo en ese viaje, regresa).

PROBLEMAS

- Hay municipios que solo recoge un contenedor

- Utiliza un nuevo camión aunque tenga viajes disponibles de otro

- Usa un viaje 2 sin haber usado el 1

Segundo MODELO

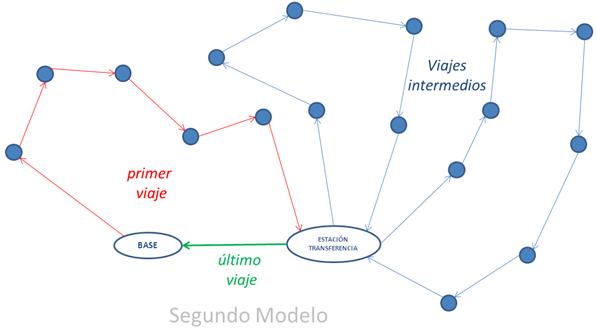
Figura 4.2: Esquema del Segundo Modelo

Consideraciones particulares del modelo:

Un esquema de este modelo podemos verlo en la figura 4.2. Seguimos tratando:

- Los vehículos comienzan y terminan su jornada en las bases, y descargan los residuos en una única Estación de Transferencia, de donde parten en el siguiente viaje.

- Consideramos la distancia recorrida y el tiempo empleado dentro de las poblaciones, base a un parámetro relacionado con el tamaño de la población y en una velocidad media única para todos los vehículos.

- La función objetivo se compone de tres sumandos: distancia recorrida total, número total de vi-sitas (modificado con un peso) y número total ve viajes (modificado con un peso).

- Las distancias entre los puntos las calculamos a partir de las coordenadas geográficas que nos entran como parámetros, es decir, son distancias geométricas.

- El tiempo medio de recogida de un contenedor lo asociamos al sistema de recogida, dependien-do por tanto del tipo de vehículo.

- Al no disponer de los tracks de los vehículos, se ha supuesto que el recorrido de los vehículos dentro de la población es nueve veces su diámetro medio.

- Al no disponer de los datos actuales de recogida, se ha supuesto que la capacidad de un conte-nedor, una vez prensado en el vehículo es inferior. Este factor de compresión se introduce como parámetro del modelo; en general 1/15.

- En este modelo consideramos las siguientes bases (ver tabla 4.2):

Base

Estaciones de Transferencia

Aracena

Condado

Cuenca Minera

Isla Cristina

Linares de la Sierra

Villarrasa

El Campillo

La Redondela

Tabla 4.2: Bases de vehículos asociadas al Segundo Modelo